La viDa es un ratico.... asi q vive , disfruta, sonrie, juega... pero Ojo... Sanamente...!!!!
sábado, 27 de noviembre de 2010
domingo, 21 de noviembre de 2010
Planeta en otra galaxia
Los astrónomos pudieron localizar el planeta, bautizado HIP 13044 b, al concentrarse en una "pequeña perturbación en la estrella causada por el tirón gravitacional de un compañero orbital",
El exoplaneta es ligeramente más grande que Júpiter, que es el mayor del Sistema Solar, y orbita alrededor de una estrella que está a 2.000 años luz de la Tierra.
Se cree que ambos, la estrella y el planeta, son parte de la corriente Helmi, un grupo de estrellas que permanece luego de que su mini-galaxia fuera absorbida por la Vía Láctea unos 9.000 millones de años atrás, señaló el estudio publicado en Science Express.
El exoplaneta (planeta que está fuera del Sistema Solar) completa un órbita cada 16 días, probablemente sea bastante caliente porque está muy cerca de la estrella y tal vez esté en el final de su vida, dijeron los astrónomos.
lunes, 15 de noviembre de 2010
Harry Potter bate récord con su ESTRENO
La primera parte de la cinta "Harry Potter y las Reliquias de la Muerte "aniquiló a la competencia en las taquillas de Norteamérica al recaudar más de US$125 millones en su fin de semana de estreno.
La película recolectó US$125,1 millones en poco más de 4.100 cines, un promedio por cine de más de 30.000 dólares, según las estimaciones del domingo.
Sin embargo, si se toma en cuenta el mayor costo de las entradas en la actualidad, la nueva película tuvo más o menos la misma recaudación. La segunda y última parte de ''Harry Potter y las Reliquias de la Muerte" se estrenará en julio.
Las seis películas anteriores sobre el joven mago británico recaudaron un total de US$5,4 mil millones en la taquilla mundial.
La primer parte de la última saga se estrenó en Londres el 11 de noviembre.
La película recolectó US$125,1 millones en poco más de 4.100 cines, un promedio por cine de más de 30.000 dólares, según las estimaciones del domingo.
Sin embargo, si se toma en cuenta el mayor costo de las entradas en la actualidad, la nueva película tuvo más o menos la misma recaudación. La segunda y última parte de ''Harry Potter y las Reliquias de la Muerte" se estrenará en julio.
Las seis películas anteriores sobre el joven mago británico recaudaron un total de US$5,4 mil millones en la taquilla mundial.
La primer parte de la última saga se estrenó en Londres el 11 de noviembre.
sábado, 13 de noviembre de 2010
Aritmetica de un computador
Binario {0,1}
Decimal {0,1,2,3,4,5,6,7,8,9}
Octal {0,1,2,3,4,5,6,7}
Hexadecimal {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}
El más conocido y usado com?nmente es el sistema de numeración decimal, pero en
computación los más utilizados son: el binario para efectuar operaciones aritmíticas,
el octal y hexadecimal para efectuar códigos intermedios que resultan mis favorables que convertir decimales a binarios o al contrario binarios
SISTEMA DECIMAL
Su origen lo encontramos en la India y fue introducido en Espa?a por los ?rabes. Su base es 10. Emplea 10 caracteres o d?gitos diferentes para indicar una determinada cantidad: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. El valor de cada s?mbolo depende de su posici?n dentro de la cantidad a la que pertenece.
SISTEMA BINARIO
Es el sistema digital por excelencia, aunque no el único, debido a su sencillez. Su base es 2 Emplea 2 caracteres: 0 y 1. Estos valores reciben el nombre de bits (dígitos binarios). As?, podemos decir que la cantidad 10011 está formada por 5 bits.
SISTEMA OCTAL
Posee ocho s?mbolos: 0, 1, 2, 3, 4, 5, 6, 7. Su base es 8. Este sistema tiene una peculiaridad que lo hace muy interesante y es que la conversi?n al sistema binario resulta muy sencilla ya que, 8 = 23 . Así, para convertir un n?mero de base 8 a binario se sustituye cada cifra por su equivalente binario en el apartado 1.5.
SISTEMA HEXADECIMAL
Est? compuesto por 16 s?mbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Su base es 16. Es uno de los sistemas m?s utilizados, ya que adem?s de simplificar la escritura de los n?meros binarios.
Hexadecimal
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
Conversión entre decimal y binario
Separar la parte entera de la parte fraccionaria.
Dividir la parte entera para 2 hasta que el ?ltimo cociente sea 1. Este ?ltimo cociente, seguidos de los sucesivos residuos le?dos de derecha a izquierda.
Octal a binario
Cada dígito octal se lo convierte en su binario equivalente de 3 bits y se juntan en el mismo orden.
La ventaja principal del sistema de numeraci?n Octal es la facilidad conque pueden realizarse la conversi?n entre un numero binario y octal. A continuaci?n mostraremos un ejercicio que ilustrará la teoría. Por medio de este tipo de conversiones, cualquier numero Octal se convierte a binario de manera individual
BINARIO- OCTAL
En esta conversi?n los n?meros tienen que ser agrupados de 3 en 3 desde la derecha y en caso de que no hubiese como agrupar al ?ltimo grupo de tres por circunstancia de que faltase n?meros se le debe aumentar los ceros que sean necesarios para completar la agrupaci?n. Luego de esto a los n?meros agrupados de tres en tres se los va sustituyendo por los n?meros que representen seg?n la tabla con el ejemplo se entender? mejor.
OPERACIONES CON NUMEROS BINARIOS
SUMA DE NUMEROS BINARIOS
1. Alinear los n?meros que desea a?adir como lo har?a si estuviera agregando n?meros decimales.
2. Comience con los dos n?meros en la columna de la derecha.
3.Suma los n?meros siguiendo las reglas de la suma decimal (1 +0 = 1, 0 +0 = 0) a menos que ambas cifras sean un 1.
4.Agregue 1+1 como "10" si est? presente. Escriba "0" y lleve adelante un "1" para sumar a la siguiente columna.
5. Comience en la pr?xima columna a la izquierda
6.Repita los pasos anteriores. Recuerde que 1 +1 = 10 y 1+1+1 = 11. Recuerde que debe llevar el "1".
suma
Ejm
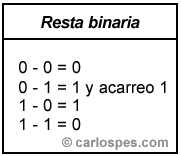
RESTA DE NUMEROS BINARIOS
Las restas b?sicas 0-0, 1-0 y 1-1 son evidentes:
* 0 - 0 = 0
* 1 - 0 = 1
* 1 - 1 = 0
* 0 - 1 = no cabe o se pide prestado al proximo.
La resta 0 - 1 se resuelve, igual que en el sistema decimal, tomando una unidad prestada de la posici?n siguiente: 10 - 1 = 1 y me llevo 1, lo que equivale a decir en decimal, 2 - 1 = 1. Esa unidad prestada debe devolverse, sum?ndola, a la posici?n siguiente. Veamos algunos ejemplos:
MULTIPLICACION DE NUMEROS BINARIOS
El algoritmo del producto en binario es igual que en n?meros decimales; aunque se lleva cabo con m?s sencillez, ya que el 0 multiplicado por cualquier n?mero da 0, y el 1 es el elemento neutro del producto.
Por ejemplo, multipliquemos

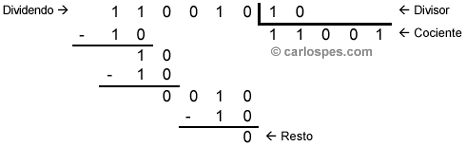
DIVISION ENTRE NUMEROS BINARIOS
La divisi?n en binario es similar a la decimal, la ?nica diferencia es que a la hora de hacer las restas, dentro de la divisi?n, estas deben ser realizadas en binario. Por ejemplo,
Decimal {0,1,2,3,4,5,6,7,8,9}
Octal {0,1,2,3,4,5,6,7}
Hexadecimal {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}
El más conocido y usado com?nmente es el sistema de numeración decimal, pero en
computación los más utilizados son: el binario para efectuar operaciones aritmíticas,
el octal y hexadecimal para efectuar códigos intermedios que resultan mis favorables que convertir decimales a binarios o al contrario binarios
SISTEMA DECIMAL
Su origen lo encontramos en la India y fue introducido en Espa?a por los ?rabes. Su base es 10. Emplea 10 caracteres o d?gitos diferentes para indicar una determinada cantidad: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. El valor de cada s?mbolo depende de su posici?n dentro de la cantidad a la que pertenece.
SISTEMA BINARIO
Es el sistema digital por excelencia, aunque no el único, debido a su sencillez. Su base es 2 Emplea 2 caracteres: 0 y 1. Estos valores reciben el nombre de bits (dígitos binarios). As?, podemos decir que la cantidad 10011 está formada por 5 bits.
SISTEMA OCTAL
Posee ocho s?mbolos: 0, 1, 2, 3, 4, 5, 6, 7. Su base es 8. Este sistema tiene una peculiaridad que lo hace muy interesante y es que la conversi?n al sistema binario resulta muy sencilla ya que, 8 = 23 . Así, para convertir un n?mero de base 8 a binario se sustituye cada cifra por su equivalente binario en el apartado 1.5.
SISTEMA HEXADECIMAL
Est? compuesto por 16 s?mbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Su base es 16. Es uno de los sistemas m?s utilizados, ya que adem?s de simplificar la escritura de los n?meros binarios.
Hexadecimal
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
Conversión entre decimal y binario
Separar la parte entera de la parte fraccionaria.
Dividir la parte entera para 2 hasta que el ?ltimo cociente sea 1. Este ?ltimo cociente, seguidos de los sucesivos residuos le?dos de derecha a izquierda.
Octal a binario
Cada dígito octal se lo convierte en su binario equivalente de 3 bits y se juntan en el mismo orden.
La ventaja principal del sistema de numeraci?n Octal es la facilidad conque pueden realizarse la conversi?n entre un numero binario y octal. A continuaci?n mostraremos un ejercicio que ilustrará la teoría. Por medio de este tipo de conversiones, cualquier numero Octal se convierte a binario de manera individual
BINARIO- OCTAL
En esta conversi?n los n?meros tienen que ser agrupados de 3 en 3 desde la derecha y en caso de que no hubiese como agrupar al ?ltimo grupo de tres por circunstancia de que faltase n?meros se le debe aumentar los ceros que sean necesarios para completar la agrupaci?n. Luego de esto a los n?meros agrupados de tres en tres se los va sustituyendo por los n?meros que representen seg?n la tabla con el ejemplo se entender? mejor.
OPERACIONES CON NUMEROS BINARIOS
SUMA DE NUMEROS BINARIOS
1. Alinear los n?meros que desea a?adir como lo har?a si estuviera agregando n?meros decimales.
2. Comience con los dos n?meros en la columna de la derecha.
3.Suma los n?meros siguiendo las reglas de la suma decimal (1 +0 = 1, 0 +0 = 0) a menos que ambas cifras sean un 1.
4.Agregue 1+1 como "10" si est? presente. Escriba "0" y lleve adelante un "1" para sumar a la siguiente columna.
5. Comience en la pr?xima columna a la izquierda
6.Repita los pasos anteriores. Recuerde que 1 +1 = 10 y 1+1+1 = 11. Recuerde que debe llevar el "1".
suma
Ejm
RESTA DE NUMEROS BINARIOS
Las restas b?sicas 0-0, 1-0 y 1-1 son evidentes:
* 0 - 0 = 0
* 1 - 0 = 1
* 1 - 1 = 0
* 0 - 1 = no cabe o se pide prestado al proximo.
La resta 0 - 1 se resuelve, igual que en el sistema decimal, tomando una unidad prestada de la posici?n siguiente: 10 - 1 = 1 y me llevo 1, lo que equivale a decir en decimal, 2 - 1 = 1. Esa unidad prestada debe devolverse, sum?ndola, a la posici?n siguiente. Veamos algunos ejemplos:
MULTIPLICACION DE NUMEROS BINARIOS
El algoritmo del producto en binario es igual que en n?meros decimales; aunque se lleva cabo con m?s sencillez, ya que el 0 multiplicado por cualquier n?mero da 0, y el 1 es el elemento neutro del producto.
Por ejemplo, multipliquemos

DIVISION ENTRE NUMEROS BINARIOS
La divisi?n en binario es similar a la decimal, la ?nica diferencia es que a la hora de hacer las restas, dentro de la divisi?n, estas deben ser realizadas en binario. Por ejemplo,
miércoles, 10 de noviembre de 2010
COMPUTADORAS PORTATILES
Portátil es un término relativo. Las primeras portátiles eran unas maletas de unos 9 kilos de peso con teclados plegables y pequeñas televisiones que actuaban a modo de monitores.
Las computadoras de bolsillo son lo bastante pequeñas. Las docking cradles para computadoras de bolsillo permiten compartir información con portátiles y Pc convencionales; este tipo de maquinas reciben el nombre de PDA (asistente digital personal).
En los década de los 90 fue el comienzo de la computadora interpersonal.
Un grupo de científicos apoyados por el gobierno de EEUU construyo una red experimental llamada ARPANET en 1969; esta red fue la más sencilla y la que dio vida a internet.
Suscribirse a:
Entradas (Atom)