Aritmetica de un computador

Binario {0,1}
Decimal {0,1,2,3,4,5,6,7,8,9}
Octal {0,1,2,3,4,5,6,7}
Hexadecimal {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}
El más conocido y usado com?nmente es el sistema de numeración decimal, pero en
computación los más utilizados son: el binario para efectuar operaciones aritmíticas,
el octal y hexadecimal para efectuar códigos intermedios que resultan mis favorables que convertir decimales a binarios o al contrario binarios

SISTEMA DECIMAL
Su origen lo encontramos en la India y fue introducido en Espa?a por los ?rabes. Su base es 10. Emplea 10 caracteres o d?gitos diferentes para indicar una determinada cantidad: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. El valor de cada s?mbolo depende de su posici?n dentro de la cantidad a la que pertenece.

SISTEMA BINARIO
 Es el sistema digital por excelencia, aunque no el único, debido a su sencillez. Su base es 2 Emplea 2 caracteres: 0 y 1. Estos valores reciben el nombre de bits (dígitos binarios). As?, podemos decir que la cantidad 10011 está formada por 5 bits.

SISTEMA OCTAL
Posee ocho s?mbolos: 0, 1, 2, 3, 4, 5, 6, 7. Su base es 8. Este sistema tiene una peculiaridad que lo hace muy interesante y es que la conversi?n al sistema binario resulta muy sencilla ya que, 8 = 23 . Así, para convertir un n?mero de base 8 a binario se sustituye cada cifra por su equivalente binario en el apartado 1.5.

SISTEMA HEXADECIMAL
Est? compuesto por 16 s?mbolos: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Su base es 16. Es uno de los sistemas m?s utilizados, ya que adem?s de simplificar la escritura de los n?meros binarios.
Hexadecimal
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
Conversión entre decimal y binario
Separar la parte entera de la parte fraccionaria.
Dividir la parte entera para 2 hasta que el ?ltimo cociente sea 1. Este ?ltimo cociente, seguidos de los sucesivos residuos le?dos de derecha a izquierda.

Octal a binario
Cada dígito octal se lo convierte en su binario equivalente de 3 bits y se juntan en el mismo orden.
La ventaja principal del sistema de numeraci?n Octal es la facilidad conque pueden realizarse la conversi?n entre un numero binario y octal. A continuaci?n mostraremos un ejercicio que ilustrará la teoría. Por medio de este tipo de conversiones, cualquier numero Octal se convierte a binario de manera individual

BINARIO- OCTAL
En esta conversi?n los n?meros tienen que ser agrupados de 3 en 3 desde la derecha y en caso de que no hubiese como agrupar al ?ltimo grupo de tres por circunstancia de que faltase n?meros se le debe aumentar los ceros que sean necesarios para completar la agrupaci?n. Luego de esto a los n?meros agrupados de tres en tres se los va sustituyendo por los n?meros que representen seg?n la tabla con el ejemplo se entender? mejor.


OPERACIONES CON NUMEROS BINARIOS

SUMA DE NUMEROS BINARIOS

1. Alinear los n?meros que desea a?adir como lo har?a si estuviera agregando n?meros decimales.
2. Comience con los dos n?meros en la columna de la derecha.
3.Suma los n?meros siguiendo las reglas de la suma decimal (1 +0 = 1, 0 +0 = 0) a menos que ambas cifras sean un 1.
4.Agregue 1+1 como "10" si est? presente. Escriba "0" y lleve adelante un "1" para sumar a la siguiente columna.
5. Comience en la pr?xima columna a la izquierda
6.Repita los pasos anteriores. Recuerde que 1 +1 = 10 y 1+1+1 = 11. Recuerde que debe llevar el "1".
suma
Ejm

RESTA DE NUMEROS BINARIOS

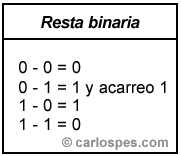
Las restas b?sicas 0-0, 1-0 y 1-1 son evidentes:
* 0 - 0 = 0
* 1 - 0 = 1
* 1 - 1 = 0
* 0 - 1 = no cabe o se pide prestado al proximo.
La resta 0 - 1 se resuelve, igual que en el sistema decimal, tomando una unidad prestada de la posici?n siguiente: 10 - 1 = 1 y me llevo 1, lo que equivale a decir en decimal, 2 - 1 = 1. Esa unidad prestada debe devolverse, sum?ndola, a la posici?n siguiente. Veamos algunos ejemplos:

MULTIPLICACION DE NUMEROS BINARIOS

El algoritmo del producto en binario es igual que en n?meros decimales; aunque se lleva cabo con m?s sencillez, ya que el 0 multiplicado por cualquier n?mero da 0, y el 1 es el elemento neutro del producto.

Por ejemplo, multipliquemos



DIVISION ENTRE NUMEROS BINARIOS
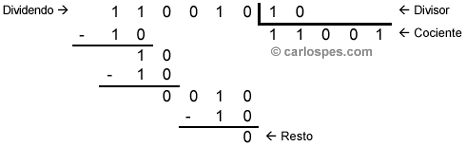
La divisi?n en binario es similar a la decimal, la ?nica diferencia es que a la hora de hacer las restas, dentro de la divisi?n, estas deben ser realizadas en binario. Por ejemplo,